How to Improve Seismic Reflector Continuity
Introduction
Event continuity, fault definition, and amplitude fidelity are key important aspects of a successful seismic interpretation. A detailed seismic interpretation, such as interpreting stratigraphic features, defining ultra-thin geobodies on a vintage land seismic data, is challenging due to pitfalls and uncertainties. There are several factors affecting the quality of seismic data, such as fold coverage, statics due to weathering zone, random and linear noises, spatial aliasing, etc. In order to enhance seismic interpretability, numerous seismic processing methods have been implemented, particularly in an effort to tackle noises such as median filter (Bednar 1983; Hall 2007). In a case of horizontal geological events, median filter is quite useful in improving seismic continuity and in tackling random noises. However, for complex and dipping geological settings, the method deteriorates structures, dipping layers, and faults. Recent developments for the implementation of median filter, for instance, have been considering step events by identifying the prime dips inside an appropriate window such as iterative dip-steered filter, which uses a Fourier radial transform in the frequency-wavenumber domain (Huo et al. 2017). As an advancement of a dip-steered filter which uses amplitudes along the tangent line of a layer, we propose layer-steered filter, using amplitudes along with the details of the layer itself. In such a way, layer-steered layer is able to attenuate random noise, improve event continuity, and reduce aliasing effects while maintaining local layer orientation and subtle structural dips. In this paper, we demonstrate the implementation of layer-steered filter on land seismic data as well as its comparison with several conventional de-noising algorithms, including dip-steered filter.
Mean filter
Mean filter is utilized to enhance the continuity of seismic layers (Bednar 1983; Hall 2007). It simply averages several seismic traces into one trace. A mean filter is also called a moving average method or instantaneous average (Hooker 1901). Mathematically, the mean filter is expressed by,
$$\overline{S}_{i} = \frac{1}{N}\mathop \sum \limits_{j = - N/2}^{N/2} S_{i + j} ,\quad i \in {\mathbb{W}},$$
(1)
where \(S_{i}\) is \(i{\text{th}}\) trace, \(\overline{S}_{i}\) is the smoothed trace, \(N\) is number of traces to be averaged, ⌊ ⌋ is floor function.
Moving average is a type of low-pass filter, but in this case, it is applied in respect of trace's number (not the time sample). From Eq. 1, it can be seen that mean smoothing averages seismic amplitudes at the same time levels. Therefore, one should be aware that the method will average seismic amplitudes from different layers regardless of its dip and layer orientation.
Median filter
In fact, the median filter cannot be linear-transformed, so it is classified as a nonlinear filter (Tukey 1977; Bednar 1983). The mathematical process of a median filter is not convolution in the time domain. As a consequence, it is not a multiplication process in the frequency domain. In general, the process is similar to the moving average. However, instead of averaging, the median filter uses the median in its calculation. For horizontal median filtering, the equation is represented by,
$$S_{\text{med}} \left( {t_{i} ,x_{j} } \right) = {\text{median}}\left( {S\left( {t_{i} , x_{k} } \right)} \right),\quad k = \left[ {j - \left\lfloor {N/2} \right\rfloor ,j + \left\lfloor {N/2} \right\rfloor } \right],\quad i,j \in {\mathbb{W}},$$
(2)
where \(N\) is the width of the median filter window (in number of samples), \(t_{i}\) is time sample, \(x_{j}\) is trace sample, \(S\left( {t_{i} ,x_{j} } \right)\) is the original seismic amplitude at \(t_{i}\) and \(x_{j}\), and \(S_{\text{med}} \left( {t_{i} ,x_{j} } \right)\) is the result of the median filter.
Meanwhile, for vertical median filtering,
$$S_{\text{med}} \left( {t_{i} ,x_{j} } \right) = {\text{median}}\left( {S\left( {t_{k} , x_{j} } \right)} \right), k = \left[ {i - \left\lfloor {N/2} \right\rfloor ,i + \left\lfloor {N/2} \right\rfloor } \right],\quad i,j \in {\mathbb{W}},\text{ }$$
(3)
Dip-steered filter
Dip-steered filter is applied neither vertically nor horizontally. The filter's orientation follows the direction of the layers, or we can say the filter is a vector. The layer's dip represents the direction of the layer. Then, the critical success of a dip-steered filter is dip determination. In this paper, the dip is determined by using the 2D Fourier transform or commonly known as \(F - K\) transform. The concept is adopted from frequency-wavenumber dip filtering (Yilmaz 2001).
Figure 1 shows a synthetic seismic section with two parallels 30° dipping layers. If we transform the seismic by using 2D Fourier transform, the strongest amplitude deviates a 30° from the vertical axis. Even though the seismic shows two layers, the 2D FFT domain only shows one strong amplitude. The benefit of the 2D FFT domain is one can obtain the dip of main layers in seismic data by considering the strongest amplitude in the FK domain. Seismic in Fig. 2 shows a 45° dipping layer and 30° dipping layers. In the 2D FFT domain, we can see two distinct lines. The deviations of the lines are 30° and 45°. It follows the layers of seismic data. However, the 30°line has a stronger amplitude than the 45° line. It is because of more layers with 30°.
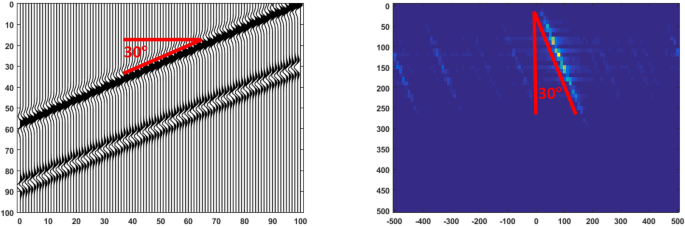
Section of seismic layers (left) and its spectrum \(F - K\) domain (right)
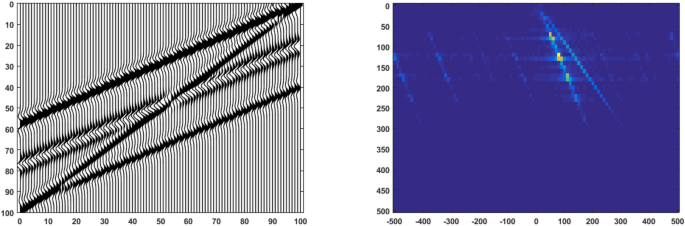
Section of seismic layers with different dips (left) and its spectrum \(F - K\) domain (right)
After the orientation of a layer is determined, we can apply a filter in that respect to layer orientation.
In the full seismic section, the dip-steered filter follows several steps:
-
Determining the size of moving window,
-
Calculating the \(F - K\) transform of seismic data in the moving window,
-
Determining the orientation (or dip) of layers in the \(F - K\) domain,
-
Applying filter in the time domain in respect of the dip. The filter can be linear or nonlinear (median). The application of this filter is inside the moving window,
-
Move the window and back to step no. 2. The movement is both in time and CDP directions.
Layer-steered filter
Layer-steered filter is in the advancement of dip-steered filter, we explained above. The dip-steered filter algorithm uses amplitudes along the tangent line of a layer, while layer-steered filter uses amplitudes along with the layer itself. In terms of layer orientation detection, the two methods use a similar approach. Figure 3 illustrates an example of an anticline structure with certain inter-bed orientations (left). The image on the right-hand side represents layer orientations measured from the figure on the left-hand side. It is very clear that values of orientation in which scaled from − 1 to + 1 represent geological events observed in the seismic section. − 1 means dipping to the left, + 1 dipping to the right, and 0 means horizontal layer. The orientation entities calculated from the data are then utilized as guidance vector for selecting samples of seismic amplitudes prior to the implementation of filter. As a result, layer-steered filter will maintain geological stratifications in any dips during the implementation of filter for enhancing seismic data quality (Fig. 4).
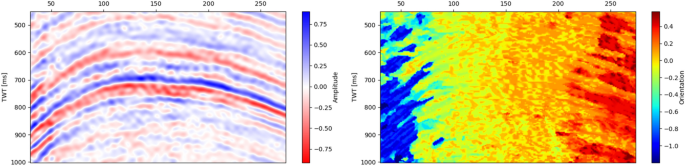
Seismic section with an anticline (left) and its measured layer's orientations (right)
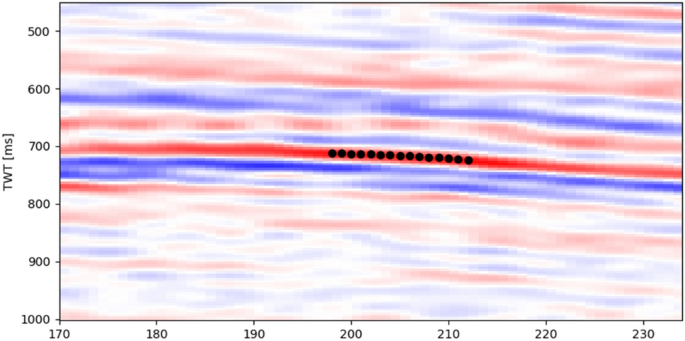
Fifteen (15) points of amplitude samples are used for filtering. Note that the samples follow the layers' orientation
Results
We implemented layer-steered filter to land seismic data. Along layer-steered filter, some conventional seismic filter methods are also implemented as comparisons (Fig. 5). The seismic data contain step dip events from CDP 200 to 400 and from CDP 670 to 780. CDP 800 to 950 are collapse zones, and CDP 950 to 1200 are relatively flat.
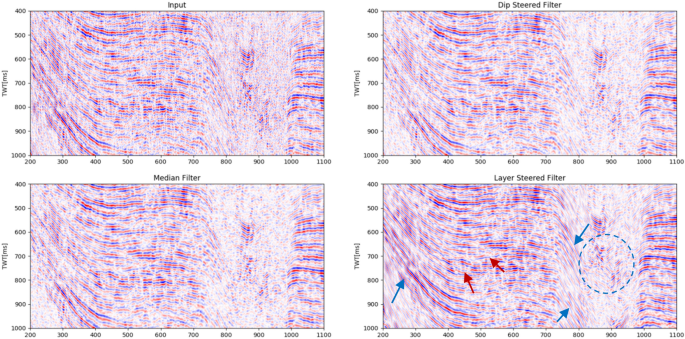
Comparison of median filter, dip-steered filter, and layer-steered filter results on land seismic data. Blue arrows indicate preserved steep dip events using layer-steered filter; the blue dash circle shows details of the internal configuration of slumping sediment
There are multiple stratigraphic play targets, such as channel cuts, submarine floor fans, and carbonate buildups. Due to low fold coverage, statics, aliasing, linear, and random noises, the interpretation is challenging, particularly in defining sequence boundaries such as onlap, downlap, channel edge, and subtle internal configuration of stratigraphic plays.
In order to enhance seismic interpretability, we implemented numerous seismic processing algorithms, including layer-steered filter. Figure 5 shows the result of layer-steered filter compared to other methods. The figure shows the superiority of layer-steered filter in terms of the preservation of primary reflectors and dips events during noise suppression and enhancement of the event. Meanwhile, median filter and dip-steered filter degrade steep dip events and features associated with dipping layers.
Figure 6 shows the corresponding FK spectrum for respected images in Fig. 5. Most random noises are fallen within seismic bandwidth of 10 to 60 Hz. Interestingly, noises are associated with higher wavenumber (cycle/m). In the FK domain of the dip-preserved filter result, it can be seen that there are cycle patterns. In this paper, dip-steered filter uses mean filter inside the process. When the mean filter is transformed into the frequency domain, it changes to be a sinc function. The sinc function causes the cycled pattern in the FK spectrum of mean filtered data. Therefore, the dip-steered filter still holds a little noise in high wavenumber. On the other hand, median filter cuts amplitude in high wavenumber. As the median filter treats noise in the time domain as outliers, it takes out the noise from seismic data. Simultaneously, high wavenumber noises are also rejected. However, even though the median filter uses the same window size as dip-steered and layer-steered, it gives narrower bandwidth than the other methods. In contrast with the median and dip-steered filter, the layer-preserved filter does not only give broader bandwidth than the median filter, but also it does not give any cycle pattern. Therefore, it is able to reject high wavenumber noises. In addition, layer-preserved filter may suppress striping patterns in the frequency direction.
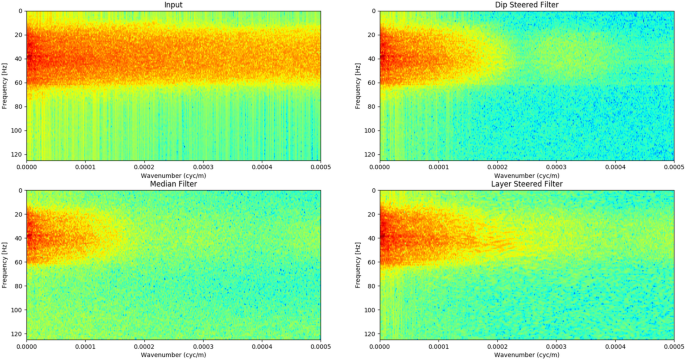
Representation of FK domain of input data, median filter, dip-steered filter, and layer-steered filter for seismic data shown in Fig. 5
Conclusion
In dealing with random noise attenuation and event continuity enhancement in dipping geological settings, layer-steered filter exhibits better behavior than median filter and dip-steered filter. Layer-steered filter performed dip orientation measurement prior to the filtering. It handles and is more sensitive to local changes. Other methods, like dip-steered filter, show less sensitive to local variations of layer orientation. Median filter does not preserve seismic amplitudes, even though the amplitudes of high dipping primary reflectors are not dim out.
Source: https://link.springer.com/article/10.1007/s13202-020-00994-2
0 Response to "How to Improve Seismic Reflector Continuity"
Post a Comment